На тарелке лежат 5 яблок и 4 апельсина сколькими способами можно выбрать один плод
Добавил пользователь Евгений Кузнецов Обновлено: 24.09.2024
Комбинаторика – это раздел математики, посвящённый решению задач выбора и расположения элементов некоторого множества в соответствии с заданными правилами. Комбинаторика изучает комбинации и перестановки предметов, расположение элементов, обладающее заданными свойствами. Обычный вопрос в комбинаторных задачах: сколькими способами….
К комбинаторным задачам относятся также задачи построения магических квадратов, задачи расшифровки и кодирования.
Рождение комбинаторики как раздела математики связано с трудами великих французских математиков 17 века Блеза Паскаля (1623–1662) и Пьера Ферма (1601–1665) по теории азартных игр. Эти труды содержали принципы определения числа комбинаций элементов конечного множества. С 50-х годов 20 века интерес к комбинаторике возрождается в связи с бурным развитием кибернетики.
Основные правила комбинаторики – это правило суммы и правило произведения.
Например, Если на тарелке лежат 5 яблок и 6 груш, то один плод можно выбрать 5 + 6 = 11 способами.
Если элемент А можно выбрать n способами, а элемент В можно выбрать m способами, то пару А и В можно выбрать n • m способами.
Например, если есть 2 разных конверта и 3 разные марки, то выбрать конверт и марку можно 6 способами (2 • 3 = 6).
Правило произведения верно и в том случае, когда рассматривают элементы нескольких множеств.
Например, если есть 2 разных конверта, 3 разные марки и 4 разные открытки, то выбрать конверт, марку и открытку можно 24 способами (2 • 3 • 4 = 24).
Произведение всех натуральных чисел от 1 до n включительно называется n – факториалом и обозначается символом n!
Например, 5! = 1 • 2 • 3 • 4 • 5 = 120.
Принято считать 0! равным 1.
Число перестановок из n равна n!
Например, если есть 3 шарика – красный, синий и зелёный, то выложить их в ряд можно 6 способами (3 • 2 • 1 = 3! = 6).
Иногда комбинаторная задача решается с помощью построения дерева возможных вариантов.
Например, решим предыдущую задачу о 3-х шарах построением дерева.
Практикум по решению задач по комбинаторике.
ЗАДАЧИ и решения
1. В вазе 6 яблок, 5 груш и 4 сливы. Сколько вариантов выбора одного плода?
6 + 5 + 4 = 15
Ответ: 15 вариантов.
2. Сколько существует вариантов покупки одной розы, если продают 3 алые, 2 алые и 4 жёлтые розы?
3. Из города А в город В ведут пять дорог, а из города В в город С ведут три дороги. Сколько путей, проходящих через В, ведут из А в С?
гласные: а, о – 2 шт.
согласные: п, л, т, к – 4 шт.2 • 4 = 8
Ответ: 8 способами.
5. Сколько танцевальных пар можно составить из 8 юношей и 6 девушек?
6. В столовой есть 4 первых блюда и 7 вторых. Сколько различных вариантов обеда из двух блюд можно заказать?
Ответ: 28 вариантов.
7. Сколько различных двузначных чисел можно составить, используя цифры 1, 4 и 7, если цифры могут повторяться?
1 цифра – 3 способа
2 цифра – 3 способа
3 цифра – 3 способа3 • 3 = 9
Ответ: 9 различных двузначных чисел.
8. Сколько различных трёхзначных чисел можно составить, используя цифры 3 и 5, если цифры могут повторяться?
1 цифра – 2 способа
2 цифра – 2 способа
3 цифра – 2 способа2 • 2 • 2 = 8
Ответ: 8 различных чисел.
9. Сколько различных двузначных чисел можно составить из цифр 0, 1, 2, 3, если цифры могут повторяться?
1 цифра – 3 способа
2 цифра – 4 способа3 • 4 = 12
Ответ: 12 различных чисел.
10. Сколько существует трёхзначных чисел, у которых все цифры чётные?
Чётные цифры – 0, 2, 4, 6, 8.
1 цифра – 4 способа
2 цифра – 5 способов
3 цифра – 5 способов4 • 5 • 5 = 100
Ответ: существует 100 чисел.
11. Сколько существует четных трёхзначных чисел?
1 цифра – 9 способов (1, 2, 3, 4, 5, 6, 7, 8, 9)
2 цифра – 10 способов (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
3 цифра – 5 способов (0, 2, 4, 6, 8)9 • 10 • 5 = 450
Ответ: существует 450 чисел.
12.Сколько различных трёхзначных чисел можно составить из трёх различных цифр 4, 5, 6?
1 цифра – 3 способа
2 цифра – 2 способа
3 цифра – 1 способ3 • 2 • 1 = 6
Ответ: 6 различных чисел.
13. Сколькими способами можно обозначить вершины треугольника, используя буквы А, В, С, D?
1 вершина – 4 способа
2 вершина – 3 способа
3 вершина – 2 способа4 • 3 • 2 = 24
Ответ: 24 способа.
14. Сколько различных трёхзначных чисел можно составить из цифр 1, 2, 3, 4, 5,при условии, что ни одна цифра не повторяется?
1 цифра – 5 способов
2 цифра – 4 способа
3 цифра – 3 способа5 • 4 • 3 = 60
Ответ: 60 различных чисел.
15. Сколько различных трёхзначных чисел, меньших 400, можно составить из цифр 1, 3, 5, 7, 9, если любая из этих цифр может быть использована только один раз?
1 цифра – 2 способа
2 цифра – 4 способа
3 цифра – 3 способа2 • 4 • 3 = 24
Ответ: 24 различных числа.
16. Сколькими способами можно составить флаг, состоящий из трёх горизонтальных полос различных цветов, если имеется материал шести цветов?
1 полоса – 6 способов
2 полоса – 5 способов
3 полоса – 4 способа6 • 5 • 4 = 120
Ответ: 120 способов.
17. Из класса выбирают 8 человек, имеющих лучшие результаты по бегу. Сколькими способами можно составить из них команду из трёх человек для участия в эстафете?
1 человек – 8 способов
2 человек – 7 способов
3 человек – 6 способов8 • 7 • 6 = 336
Ответ: 336 способов.
18. В четверг в первом классе должно быть четыре урока: письмо, чтение, математика и физкультура. Сколько различных вариантов расписания можно составить на этот день?
1 урок – 4 способа
2 урок – 3 способа
3 урок – 2 способа
4 урок – 1 способ4 • 3 • 2 • 1 = 24
Ответ: 24 варианта.
19. В пятом классе изучаются 8 предметов. Сколько различных вариантов расписания можно составить на понедельник, если в этот день должно быть 5 уроков и все уроки разные?
1 урок – 8 вариантов
2 урок – 7 вариантов
3 урок – 6 вариантов
4 урок – 5 вариантов
5 урок – 4 варианта8 • 7 • 6 • 5 • 4 = 6720
Ответ: 6720 вариантов.
20. Шифр для сейфа составляется из пяти различных цифр. Сколько различных вариантов составления шифра?
1 цифра – 5 способов
2 цифра – 4 способа
3 цифра – 3 способа
4 цифра – 2 способа
5 цифра – 1 способ5 • 4 • 3 • 2 • 1 = 120
Ответ: 120 вариантов.
21. Сколькими способами можно разместить 6 человек за столом, на котором поставлено 6 приборов?
6 • 5 • 4 • 3 • 2 • 1 = 720
Ответ: 720 способов.
22. Сколько вариантов семизначных телефонных номеров можно составить, если исключить из них номера, начинающиеся с нуля и 9?
1 цифра – 8 способов
2 цифра – 10 способов
3 цифра – 10 способов
4 цифра – 10 способов
5 цифра – 10 способов
6 цифра – 10 способов
7 цифра – 10 способов8 • 10 • 10 • 10 • 10 • 10 • 10 = 8.000.000
Ответ: 8.000.000 вариантов.
23. Телефонная станция обслуживает абонентов, у которых номера телефонов состоят из 7 цифр и начинаются с 394. На сколько абонентов рассчитана эта станция?
№ телефона 394
10 • 10 • 10 • 10 = 10.000
Ответ: 10.000 абонентов.
24. Имеется 6 пар перчаток различных размеров. Сколькими способами можно выбрать из них одну перчатку на левую руку и одну перчатку на правую руку так, чтобы эти перчатки были различных размеров?
Левые перчатки – 6 способов
Правые перчатки – 5 способов (6 перчатка того же размера, что и левая)6 • 5 = 30
Ответ: 30 способов.
25 . Из цифр 1, 2, 3, 4, 5 составляют пятизначные числа, в которых все цифры разные. Сколько таких чётных чисел?
5 цифра – 2 способа (две чётные цифры)
4 цифра – 4 способа
3 цифра – 3 способа
2 цифра – 2 способа
1 цифра – 1 способ2 • 4 • 3 • 2 • 1 = 48
Ответ: 48 чётных чисел.
26. Сколько существует четырёхзначных чисел, составленных из нечётных цифр и делящихся на 5?
Нечётные цифр – 1, 3, 5, 7, 9.
Из них делятся на 5 – 5.
4 цифра – 1 способ (цифра 5)
3 цифра – 4 способа
2 цифра – 3 способа
1 цифра – 2 способа1 • 4 • 3 • 2 = 24
Ответ: 24 числа.
27. Сколько существует пятизначных чисел, у которых третья цифра – 7, последняя цифра – чётная?
1 цифра – 9 способов (все, кроме 0)
2 цифра – 10 способов
3 цифра – 1 способ (цифра 7)
4 цифра – 10 способов
5 цифра – 5 способов (0, 2, 4, 6, 8)9 • 10 • 1 • 10 • 5 = 4500
Ответ: 4500 чисел.
28. Сколько существует шестизначных чисел, у которых вторая цифра – 2, четвёртая – 4, шестая – 6, а все остальные – нечётные?
1 цифра – 5 вариантов (из 1, 3, 5, 7, 9)
2 цифра – 1 вариант (цифра 2)
3 цифра – 5 вариантов
4 цифра – 1 вариант (цифра 4)
5 цифра – 5 вариантов
6 цифра – 1 вариант (цифра 6)5 • 1 • 5 • 1 • 5 • 1 = 125
Ответ: 125 чисел.
29.Сколько различных чисел, меньших миллиона, можно записать с помощью цифр 8 и 9?
Однозначных – 2
Двузначных – 2 • 2 = 4
Трёхзначных – 2 • 2 • 2 = 8
Четырёхзначных – 2 • 2 • 2 • 2 =16
Пятизначных – 2 • 2 • 2 • 2 • 2 = 32
Шестизначных – 2 • 2 • 2 • 2 2 • 2 = 64Всего: 2 + 4 + 8 + 16 + 32 + 64 = 126
Ответ: 126 чисел.
30. В футбольной команде 11 человек. Нужно выбрать капитана и его заместителя. Сколькими способами это можно сделать?
Капитан – 11 способов
Заместитель – 10 способов11 • 10 = 110
Ответ: 110 способов.
31.В классе учатся 30 человек. Сколькими способами из них можно выбрать старосту и ответственного за проездные билеты?
Староста – 30 способов
Ответ. за билеты – 29 способов30 • 29 = 870
Ответ: 870 способов.
32. В походе участвуют 12 мальчиков, 10 девочек и 2 учителя. Сколько вариантов групп дежурных из трёх человек (1 мальчик, 1 девочка, 1 учитель) можно составить?
12 • 10 • 2 = 240
Ответ: 240 способов.
33. Сколько комбинаций из четырёх букв русского алфавита (в алфавите всего 33 буквы) можно составить при условии, что 2 соседние буквы будут разными?
1 буква – 33 способа
2 буква – 32 способа
3 буква – 32 способа
4 буква – 32 способа33 • 32 • 32 • 32 = 1.081.344
Ответ: 1.081.344 комбинаций.
В обыденной жизни нам нередко встречаются задачи, которые имеют несколько различных вариантов решения. Чтобы сделать правильный выбор, важно не упустить ни один из них. Для этого надо уметь осуществлять перебор всех возможных вариантов или подсчитывать их число. Задачи, требующие такого решения называются комбинаторными.
Комбинаторные задачи в начальном курсе систематически решаются как правило, методом перебора. Для облегчения этого процесса нередко используются таблицы и графы. В связи с этим учителю начальных классов необходимы определенные навыки решения комбинаторных задач. Прежде всего, он должен, решая несложные комбинаторные задачи, уметь грамотно осуществлять перебор всевозможных вариантов и при этом быть уверенным в том, что перебор осуществлен правильно. Учителю надо знать общие правила комбинаторики (суммы, произведения), некоторые виды комбинаций, число которых может быть подсчитано с помощью формул.
Впервые во 2 классе II часть Ур. 37-42. К настоящему времени дети уже достаточно подготовлены к усвоению мысли о целесообразности упорядоченного перебора правила суммы и произведения.
Задача: На тарелке лежит 5 яблок и 4 апельсина. Сколькими способами можно выбрать один плод?
Так как в задаче речь идет о выборе либо яблок, либо апельсинов, то согласно правилу суммы, можно осуществить 5 + 4 = 9 способом.
2. Правило произведения – для нахождения элементов в декартовом произведении. Если объект а можно выбрать m способом, а объект а, в – k способом, то пару (а,в)можно выбрать – m х k способом.
Задача1: На тарелке 5 яблок и 4 апельсина. Сколькими способами можно выбрать пару плодов из апельсинов и яблок.
Решение, т.к. речь идет о выборе пары (яблоки, апельсины), то согласно правилу произведения 4 х 5 = 20 способов.
Задача 2: Сколько трехзначных чисел можно составить, используя цифры 7,4,5?
Решение: О подсчете числа наборов из трех элементов (кортеш), согласно правилу произведения получим 3 х 3 х 3 = 27 способов.(т.к. цифры в записи числа могут повторяться, то цифру сотен, цифру десятков и цифру единиц можно подобрать 3 разными способами каждую.)
Задача. Сколько всего четырехзначных чисел можно составить из цифр 0 и 3?
Решение. Запись четырехзначного числа представляет собой упорядоченный набор (кортеж) из четырех цифр. Первую цифру - цифру тысяч можно выбрать только одним способом, так как запись числа не может начинаться с нуля. Цифрой сотен может быть либо ноль, либо три, т.е. имеется два способа выбора. Столько же способов выбора имеется для цифры десятков и цифры единиц.
Итак, цифру тысяч можно выбрать одним способом, цифру сотен - двумя, цифру десятков - двумя, цифру единиц - двумя. Чтобы узнать, сколько всего четырехзначных чисел можно составить из цифр 0 и 3, согласно правилу произведения, способы выбора каждой цифры надо перемножить: 1х2х2х2 = 8.
Таким образом, имеем 8 четырехзначных чисел.
Задача . Сколько трехзначных чисел можно записать, используя цифры 0, 1, 3, 6, 7 и 9, если каждая из них может быть использована в записи только один раз?
Решение. Так как запись числа не может начинаться с нуля, то цифру сотен можно выбрать пятью способами; выбор цифры десятков можно осуществить также пятью способами, поскольку цифры в записи числа не должны повторяться, а одна из шести данных цифр будет уже использована для записи сотен; после выбора двух цифр (для записи сотен и десятков) выбрать цифру единиц из данных шести можно четырьмя способами. Отсюда, по правилу произведения, получаем, что трехзначных чисел (из данных шести цифр) можно образовать 5х5х4= 100 способами.
Дерево возможностей – наиболее универсальное средство для поиска решения.
Типовые примеры
Пример. В вазе для фруктов лежало 6 яблок, 5 груш и 4 персика. Сколькими способами можно выбрать один плод для угощения?
6 + 5 + 4 = 15 (способов).
Пример. Нужно купить подарок для первоклассника, состоящий из ранца, пенала, подставки для книг и дневника. Сколькими способами это можно сделать, если магазин предлагает 4 вида ранцев, 5 видов пеналов, 3 вида подставок и 2 вида дневников?
4 • 5 • 3 • 2 = 120 (способами).
1. Сколько различных двузначных чисел можно записать, используя цифры 3, 4, 5 и 6? Сколько различных двузначных чисел можно записать, используя при записи числа каждую из указанных цифр только один раз? Запишите эти числа.
4. Сколько трехзначных чисел можно составить из трех различных, не равных нулю цифр? Зависит ли результат от того, какие цифры взяты? Укажите какой-нибудь способ перебора трехзначных чисел, при котором ни одно число не может быть пропущено.
Сколько всевозможных трехзначных чисел можно составить из цифр 1, 2, 3 и 4 так, чтобы цифры в записи числа не повторялись? Изменится ли решение этой задачи, если вместо цифры 4 будет дана цифра О?
4. Сколько всевозможных четырехзначных чисел можно составить, используя для записи цифры 1, 2, 3 и 4? Какова разность между самым большим и самым маленьким из них?
5. Сколько пятизначных чисел, первые (слева) три цифры которых 2, 3 и 4, можно составить из цифр 1, 2, 3, 4, 5? Изменится ли ответ в этой задаче, если цифры в записи числа не будут повторяться?
6. Из цифр 0, 1, 2, 3, 4 составляют всевозможные пятизначные числа, причем так, что в записи каждого числа содержатся все данные цифры. Сколько можно составить таких чисел? Чему будет равна разность между наибольшим и наименьшим из полученных чисел?
7. Сколько натуральных чисел, меньших 1000, можно записать, используя цифры 7, 4 и 5? Сколько среди них четных? Нечетных? Кратных 5?

Комбинаторика – это раздел математики, посвящённый решению задач выбора и расположения элементов некоторого множества в соответствии с заданными правилами

Комбинаторика – это раздел математики, посвящённый решению задач выбора и расположения элементов некоторого множества в соответствии с заданными правилами. Комбинаторика изучает комбинации и перестановки предметов, расположение элементов, обладающее заданными свойствами. Обычный вопрос в комбинаторных задачах: сколькими способами….
К комбинаторным задачам относятся также задачи построения магических квадратов, задачи расшифровки и кодирования.
Задача На блюде 7 яблок, 4 мандарина и 5 груш

На блюде 7 яблок, 4 мандарина и 5 груш. Найдите количество способов, которыми можно взять с блюда
а) один плод;
б) грушу и мандарин;
в) яблоко и грушу;
г) яблоко и мандарин;
д) два фрукта с различными названиями.
В вазе лежат 3 яблока и 5 груш
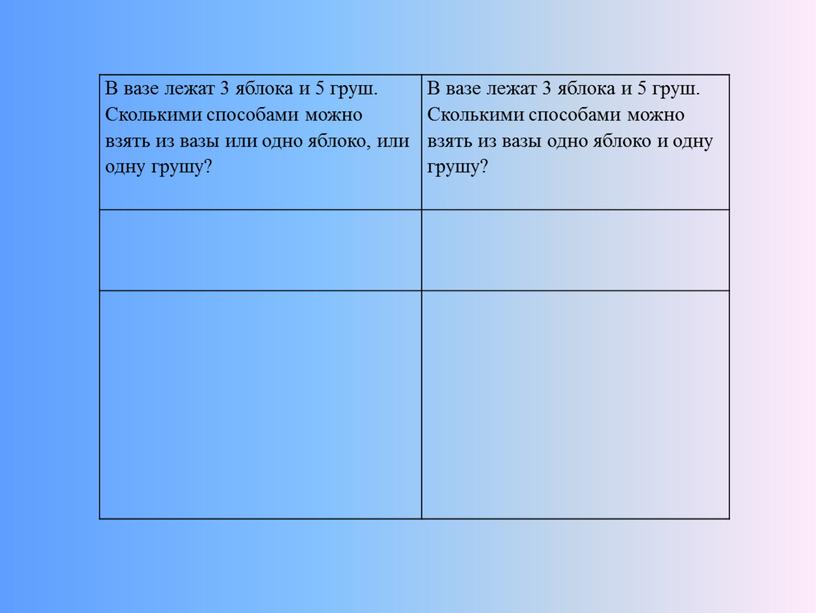
В вазе лежат 3 яблока и 5 груш. Сколькими способами можно взять из вазы или одно яблоко, или одну грушу?
В вазе лежат 3 яблока и 5 груш. Сколькими способами можно взять из вазы одно яблоко и одну грушу?
В вазе лежат 3 яблока и 5 груш
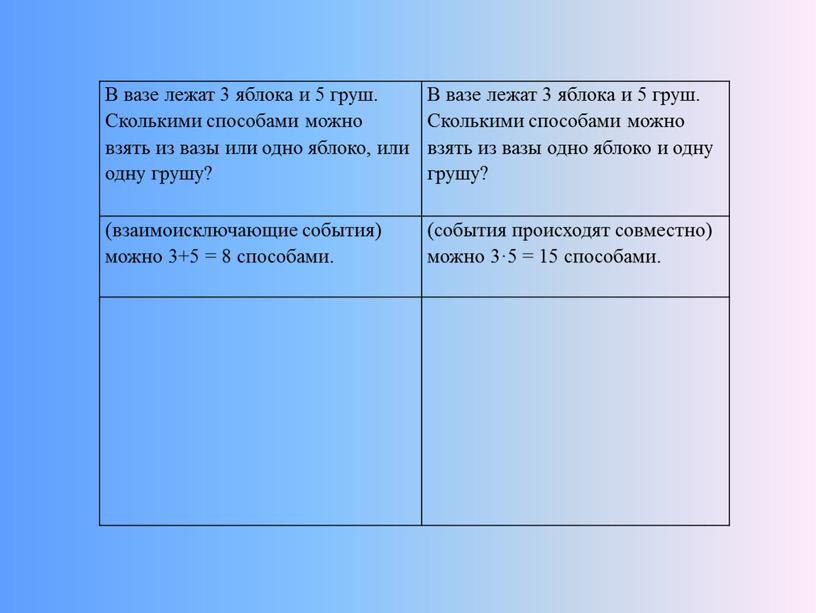
В вазе лежат 3 яблока и 5 груш. Сколькими способами можно взять из вазы или одно яблоко, или одну грушу?
В вазе лежат 3 яблока и 5 груш. Сколькими способами можно взять из вазы одно яблоко и одну грушу?
(взаимоисключающие события) можно 3+5 = 8 способами.
(события происходят совместно) можно 3·5 = 15 способами.
В вазе лежат 3 яблока и 5 груш
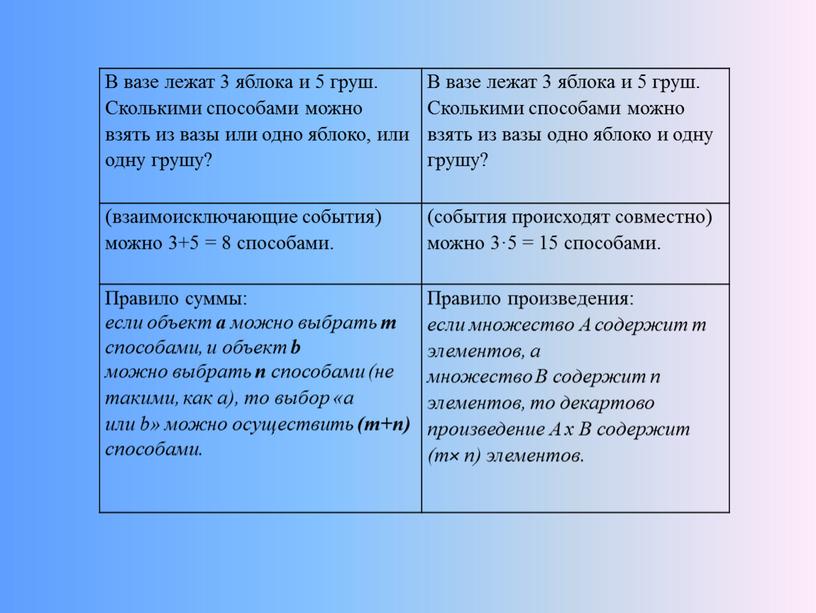
В вазе лежат 3 яблока и 5 груш. Сколькими способами можно взять из вазы или одно яблоко, или одну грушу?
В вазе лежат 3 яблока и 5 груш. Сколькими способами можно взять из вазы одно яблоко и одну грушу?
(взаимоисключающие события) можно 3+5 = 8 способами.
(события происходят совместно) можно 3·5 = 15 способами.
Правило произведения:
если множество А содержит m элементов, а
множество В содержит n элементов, то декартово
произведение А х В содержит (m× n) элементов.
Задача 1: На тарелке лежат 6 яблок и 4 апельсина

Задача 1: На тарелке лежат 6 яблок и 4 апельсина. Сколькими способами можно выбрать один плод?
Задача 2: Из Красноярска в Канск ведут три дороги, а из

Задача 2: Из Красноярска в Канск ведут три дороги, а из Канска в Абан – 4 дороги. Сколько различных путей ведут из Красноярска в Абан, если прямой дороги из Красноярска в Абан нет?
Задача 3: В чемпионате мира участвуют 18 команд по футболу

Задача 3: В чемпионате мира участвуют 18 команд по футболу. Сколькими способами можно распределить золотые, серебряные и бронзовые комплекты?
Есть 5 книг. Сколькими способами их можно расположить на книжной полке? 2)

1) Есть 5 книг. Сколькими способами их можно расположить на книжной полке? 2) В семье шесть человек, а за столом в кухне шесть стульев. Было решено каждый вечер перед ужином, рассаживаться на эти стулья по- новому. Сколько дней члены семьи смогут делать это без повторений?
N! - обозначение, которое используют для краткой записи произведения всех натуральных чисел от 1 до n включительно и называют "n-факториал"

N! - обозначение, которое используют для краткой записи произведения всех натуральных чисел от 1 до n включительно и называют "n-факториал"
Рефлексия • Сегодня я узнал… •

• Сегодня я узнал…
• Было интересно…
• Было трудно…
• Я выполнял задания…
• Теперь я могу…

120 № 5912
На блюде лежат 7 яблок, 3 груши и 4 апельсина. Найдите количество способов, которыми можно взять с блюда: а) один плод; б) яблоко и грушу; в) выбрать яблоко и апельсин; г) выбрать грушу и апельсин; д) выбрать два фрукта с разными названиями?
а) Всего на блюде 7 + 3 + 4 = 14 фруктов, один из них можно взять 14 способами.
б) Вместе с каждым из 7 яблок можно взять одну из 3 груш, поэтому всего способов взять яблоко и грушу 7 · 3 = 21.
в) Вместе с каждым из 7 яблок можно взять один из 4 апельсинов, поэтому всего способов взять яблоко и апельсин 7 · 4 = 28.
г) Вместе с каждой из 3 груш можно взять один из 4 апельсинов, поэтому всего способов взять грушу и апельсин 3 · 4 = 12.
д) Чтобы получить количество способов выбрать два фрукта с разными названиями, нужно сложить количество способов из пунктов б), в) и г). Получим 21 + 28 + 12 = 61 способ.
Читайте также:

