Последовательность чисел фибоначчи описывает размножение кроликов рост веток на деревьях

Добавил пользователь Владимир З.
Обновлено: 19.09.2024

Числа Фибоначчи в Европе популяризовал Леонардо Пизанский (по прозвищу Фибоначчи – сын Боначчи), в задаче о кроликах:

Пусть в огороженном месте имеется пара кроликов (самка и самец) в первый день января. Эта пара кроликов производит новую пару кроликов (самку и самца) в первый день февраля и затем в первый день каждого следующего месяца. Каждая новорожденная пара кроликов становится зрелой уже через месяц и затем через месяц дает жизнь новой паре кроликов. Возникает вопрос: сколько пар кроликов будет в огороженном месте через год, то есть через 12 месяцев с начала размножения.

Оказывается, число кроликов по месяцам описывается последовательностью

В ней каждое число равно сумме двух предыдущих. Условия задачи все равно нереалистичны, так что можно не стесняться: предположить, что кролики бессмертны, и продолжить последовательность до бесконечности:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269, 2178309, 3524578, 5702887, 9227465, 14930352, 24157817, 39088169, 63245986, 102334155, ….

Есть свидетельства, что последовательность задолго до Леонардо была известна в Индии, и что в честь Фибоначчи ее назвал Эдуард Люка.

Про экспоненциальный рост

Как мы видим, последовательность очень быстро растет (экспоненциально, как последовательность степеней). Примерно как 1, 2, 4, 8, 16, 32, … или 1, 10, 100, 1000, … (тоже экспоненциальный рост.) Экспоненциальный рост вообще встречается в природе и в приложениях: так растут популяции, капиталы в банке, число радиоактивных атомов и число зерен на шахматной доске (Вы же помните легенду про жадного султана и бедного изобретателя шахмат ;))

В природе экспоненциальный рост имеет место лишь приблизительно и только в некоторых пределах.

Красивые фотографии

Последовательности в природе, напоминающие Фибоначчи, тоже похожи на Фибоначчи только приблизительно и в некоторых пределах. Широко известны примеры из мира растений: семена подсолнуха, сосновые шишки, лепестки цветков, ячейки ананаса. Видимо, здесь задействован один механизм (я скопировала первую попавшуюся картинку из интернета):

Отчасти популярность чисел Фибоначчи связана с такими красивыми картинками. В интернете их полным-полно.

А вот скажем, закон радиоактивного распада не менее поразителен, история его открытия драматична, человечество поставило его себе на службу… но он не так популярен в СМИ. Нет для него таких красивых картинок, да и описывается он дифференциальным уравнением, а любителей дифференциальных уравнений меньше, чем любителей красивых картинок.

В математике

В математике бывают объекты, которые задаются очень просто, но показывают удивительно сложные и многогранные связи между своими компонентами. Например: треугольник в планиметрии, конические сечения, треугольник Паскаля, простые числа, … Они завораживают нас как картинки в калейдоскопе. Чуть повернешь – и открываются новые узоры, новые свойства. Числа Фибоначчи –один из таких объектов. Каждый математик на пути в науку их обязательно встречал.

Чтобы перечислить все их удивительные свойства, нужна отдельная книга (и кстати, выходит журнал с таким названием, посвященный одним только числам Фибоначчи). Скажу только, что отношение каждого числа Фибоначчи к предыдущему приближает золотое сечение, и чем числа больше, тем приближение лучше.

Почему же математики выделили числа Фибоначчи в отдельную группу чисел

Специалист по теории чисел Леопольд Кронекер считал, что только одна из них создана Богом (и это вовсе не последовательность Фибоначчи, а другая, на сайте ее номер 27), а остальные – дело рук человеческих.

В целом журналисты несколько преувеличивают значимость чисел Фибоначчи: они, безусловно, прекрасны, но стоят в одном ряду с многими другими не менее прекрасными и полезными математическими объектами.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Муниципальное бюджетное образовательное

учреждение средняя школа №9 городского округа город Выкса Нижегородской области

Числа Фибоначчи

в живой и неживой природе

Физико-математическое отделение

Секция математическая

Работу выполнила:

ученица 8 В класса

Научный руководитель:

Учитель МБОУ СШ №9

Залугина Мария Вадимовна

При работе над данной темой мной было рассмотрено множество примеров использования чисел Фибоначчи. Работа состоит из 3 частей. Первая часть содержит биографию Леонардо Пизанского и историю возникновения данных чисел. Вторая и третья непосредственно примеры использования чисел в живой и неживой природе. В ходе работы над темой было проведено анкетирование учащихся с целью выявления детей, знающих о числах Фибоначчи.

Цель работы: изучить проявление чисел Фибоначчи, найти примеры использования чисел Фибоначчи.

Задачи работы:

Описать способ построения ряда Фибоначчи.

Увидеть математические закономерности вокруг нас

Объект исследования: математические абстракции, созданные человеком, окружающий растительный и животный мир.

Предмет исследования: форма и строение исследуемых предметов и явлений.

Методы исследования:

Эмпирический (наблюдение, эксперимент, измерение).

Теоретический (логическая ступень познания).

Актуальность исследования: открытие чисел Фибоначчи в окружающей нас действительности.

Практическая значимость: использование приобретенных знаний и навыков исследовательской работы при изучении других школьных предметов.

Гуляя по просторам интернета я наткнулась на статью о числах Фибоначчи, в первую очередь меня заинтересовало странное название, а зачем мне захотелось узнать, где же эти числа применяются.

Я обратилась к научной литературе и прочитала о числах Фибоначчи, о магических числах, которые таят в себе великую загадку. Оказывается, эти числа можно найти в подсолнухах и сосновых шишках, в крыльях стрекозы и морских звёздах, в строение человеческого тела и в музыкальных ритмах.

Почему же эта последовательность чисел столь распространена в нашем мире?

Результатом моей деятельности и явилась данная исследовательская работа.

1.1 Биография Леонардо Пизанского

Точная дата его рождения неизвестна. Предположительно Фибоначчи родился в 1170г. в городе Пиза, в Италии. Леонардо из Пизы, известный как Фибоначчи, был первым из великих математиков Европы позднего Средневековья. Будучи рожденным в Пизе в богатой купеческой семье, он пришел в математику благодаря сугубо практической потребности установить деловые контакты.

На протяжении нескольких столетий по труду Фибоначчи ученые знакомились с двумя важнейшими разделами математики – арифметикой и алгеброй и черпали из него задачи и оригинальные методы решения, благодаря чему уже в XV – XVI в.в. те разошлись по многочисленным итальянским, французским, немецким, английским, а позже и русским рукописям, печатным книгам и учебникам.

Когда Леонардо вернулся в Италию, там правил император Фридрих II. Он не признавал рыцарские турниры, вместо них он проводил гораздо менее кровавые математические соревнования, на которых противники обменивались не ударами, а задачами. На таких турнирах и заблистал талант Леонардо Фибоначчи.

Предположительно Фибоначчи умер во время одного из Крестовых походов в 1228 году, сопровождая императора Фридриха II.

1.2 История ряда Фибоначчи

Леонардо Фибоначчи совершил открытие чисел (впоследствии названных его именем) случайно. В 1202 году он пытался решить практическую задачу: какой максимальный приплод может дать одна пара кроликов за год и создать формулу, описывающую последовательность их размножения.

Рисунок 1 - Леонардо Фибоначчи (Пизанский)

Он пытался создать формулу, описывающую последовательность размножения кроликов (рисунок 2).

Рисунок 2 – Последовательность размножения кроликов

Разгадкой стал числовой ряд, каждое последующее число которого, является суммой двух предыдущих: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584 и т.д.

Закон образования членов этого ряда следующий :

Первые два члена являются единицами (1), а каждый последующий член равен сложению двух чисел ему предшествующих:

S _n = S _n _-1 + S _n _-2

Например: 1+1 = 2; 1 + 2 = 3; 3 + 5 = 8; 5 + 8 = 13 и т.д.

Числа, образующие данную последовательность называются "числами Фибоначчи", а сама последовательность - последовательностью Фибоначчи.

У числового ряда Фибоначчи есть интересная особенность:

каждое третье число Фибоначчи четно;

каждое четвертое кратно 3;

каждое пятнадцатое оканчивается нулем;

Фибоначчи вёл отшельнический образ жизни, много времени проводил на природе, и, гуляя в лесу, он обратил внимание, что эти числа стали буквально преследовать его. Повсюду в природе он снова и снова встречал эти числа. Например, лепестки и листья растений строго укладывались в данный числовой ряд.

Учёные, анализируя применение числового ряда к природным феноменам и процессам, обнаружили, что эти числа содержатся буквально во всех объектах живой природы, в растениях, в животных и в человеке.

Удивительно, что последовательность чисел Фибоначчи напрямую связана со спиральность в окружающем мире.

Рассмотрим примеры, где встречаются числа Фибоначчи в живой и неживой природе.

Если посмотреть на растения и деревья вокруг нас, то видно, сколь много листьев на каждом из них. Издалека, кажется, что ветки и листья на растениях расположены случайным образом, в произвольном порядке. Однако во всех растениях чудесным образом, математически точно спланировано какая веточка, откуда будет произрастать, как ветки и листья будут располагаться около стебля или ствола. Ни один лист, ни один цветок не появляется случайно. Ещё до появления растение уже точно запрограммировано. Совместная работа ботаников и математиков пролила свет на эти удивительные явления природы. Выяснилось, что в расположении листьев на ветке, в числе оборотов на стебле, в числе листьев в цикле проявляет себя ряд Фибоначчи .

Если вы зададитесь целью отыскать числовые закономерности в живой природе, то заметите, что эти числа часто встречаются в различных спиральных формах, которыми так богат мир растений. Например, черенки листьев примыкают к стеблю по спирали, которая проходит между двумя соседними листьями: 1/3 полного оборота - у орешника, 2/5 - у дуба, 3/8 - у тополя и груши, 5/13 - у ивы.

Семена подсолнечника, эхинацеи пурпурной и многих других растений, расположены спиралями, причем количества спиралей каждого направления - числа Фибоначчи.

Подсолнечник имеет 21 и 34 спираль, а цветок эхинацеи - 34 и 55.

Рисунок 3 – Подсолнечник и цветок эхинацеи

Чёткая, симметричная форма цветов также подчинена строгому закону. У многих цветов количество лепесточков – именно числа из ряда Фибоначчи. Например: цветок ирис имеет 3лепетка; лютик -5; златоцвет -8; дельфиниум – 13 (рисунок 4).

Рисунок 4 - Цветы ирис, лютик, златоцвет, дельфиниум

Другим примером являются цветы ромашки, у которых имется 21 лепесток; у астры – 34; у маргаритки – 55 (рисунок 5).

Рисунок 5 - Цветы ромашки, астры, маргаритки

Числа Фибоначчи проявляются в морфологии различных организмов. Например, морские звезды. Число лучей у них отвечает ряду чисел Фибоначчи и равно 5, 8, 13, 21, 34, 55 (рисунок 5).

Рисунок 5 – Морские звезды

Рассмотрим спираль так же можно в паутине и в разных явлениях природы, например таких как: смерч, ураган, облака, морские волны. Наша галактика – это спираль (рисунок 6).

Рисунок 6 – Спираль Фибоначчи в природе

Рисунок 7 – Спираль Фибоначчи в космическом пространстве

Числовой ряд Фибоначчи присутствует в живой и неживой природе, окружающей нас (цветы, морские обитатели, волны, космос и т.д.).

2.1 Числа Фибоначчи в изобретениях человека.

Подсмотрев у природы закон, выраженный последовательностью чисел Фибоначчи, учёные и люди искусства стараются подражать ему, воплощать этот закон в своих творениях.

Наблюдая за явлениями, происходящими в природе, учёные сделали поразительные выводы о том, что вся последовательность событий, происходящих в жизни, революции, крушения, банкротства, периоды процветания, законы и волны развития на фондовом и валютных рынках, циклы семейной жизни, и так далее, организуются на временной шкале в виде циклов, волн (рисунок 8). Эти циклы и волны тоже распределяются в соответствии с числовым рядом Фибоначчи!

Опираясь на эти знания, человек научится в будущем прогнозировать различные события и управлять ими.

Рисунок 8 – Цикличность жизненный событий

3.1 Деление сторон квадрата на части по закону чисел Фибоначчи

Для проведения данного исследования был рассмотрен числовой ряд Фибоначчи: 1,1,2,3,5,8,13,21…., из которого была выбрана цифра. К примеру, число 13 условных единиц будет являться длинной стороны квадрата, следовательно, его площадь будет равна 169 условных единиц (рисунок 9).

Рисунок 9 – Квадрат со значениями сторон и площадью

Рисунок 10 – Деление квадратов на части по закону чисел Фибоначчи

Затем одна сторона квадрата была разделена на две части, длины которых соответствуют двум числам Ряда Фибоначчи. Это числа 5 и 8, которые соответствуют ряду Фибоначчи.

В моем примере соседние значения от числа 13 в числовой последовательности Фибоначчи являются 8 и 21. Их можно получить следующим образом: 13 – 5 = 8 и 13 + 9 = 21. Произведение этих чисел равно: 21х8 = 168 условных единиц.

Таким образом, условие деления квадрата по закону чисел Фибоначчи выполняется: 13 2 – 21х8 = 169 – 168 = 1. В итоге мы получаем разницу числе в единицу.

Анализируя результаты опыта, можно сделать вывод, что свойство деления квадратов, выведенное Фибоначчи, имеет определенную систему и закономерность, которую можно доказать опытным путем.

Царице математике – одной из вечных обучающих и прикладных наук, послужило много мудрых, одержимых творцов. В теорию чисел, множеств, комбинаторику привнес немалый вклад Леонардо Пизанский. Вызывают интерес и любопытство загадки золотого сечения – гармонических пропорций в окружающем мире. Числа Фибоначчи раскрывают тайны и закономерности отношений в различных явлениях со времени открытия и до современности.

Что такое ряд чисел Фибоначчи

1 +
1 +
=	2 +
=	3 +
=	5 +
=	8 +
=	13 +
=	21, 34, 55, 89, 144,…

Формула получения элемента m последовательности Фибоначчи: L(m) = L(m-1) + L(m-2), где m любой натуральный целый индекс. Поэтому элементы ряда четные следуют через 2 элемента нечетных (сумма 2-ух нечетных равна четному, а четного с нечетным равна нечетному).

В ряду натуральных чисел, первые два — единицы, но иногда применяется это множество, начинающееся с 0 и 1.

Некоторые удивительные математические свойства элементов ряда:

Задача с кроликами

На подсчет элементов забавной числовой последовательности Фибоначчи натолкнули плодовитые кролики. Ученый не изучает явление со всех сторон сразу. Определяются начальные характерные условия, ограничивается круг основных влияющих факторов, а незначительные опускаются, допускаются поправки. Так составили знаменитую задачу про биологически нереальное размножение кроликов, суть излагается не дословно.

В доме появилась пара маленьких крольчат, мальчик и девочка. Нужно определить, сколько пар зверушек будет через 12 месяцев. Надо учесть, что в первый месяц жизни они бездетны. Пара малюток первых (самка и самец) прибавляется во 2-ой месяц, а уже дальше парочки длинноухих ежемесячно нарождаются. Кролики не умирают, а превышающая плодовитость не учитывается.

Для упрощения обозначения можно принять месяц – м., число пар кроликов – это =1. Решается последовательно по шагам, пока математик не подметил закономерности чисел:

1 м. пара маленьких=1.
2 м. только первая пара= 1.
3 м. парочка дала приплод 1 пару=2.
4 м. старые двое рождают новую двойню, второй парочке еще рановато=3.
5 м. первая парочка приносит ещё пару, вторая плодит новую двойню, третьей паре рано=5.
6 м. 5+3=8, 55+34=89(11), 89+55=144(12)

По ежемесячным результатам получились числа Фибоначчи. После 12 месяцев расплодится длинноухих 144(12м.)+89(11м.)=233 пары. Получилась первичная модель экспоненциального роста кроличьей популяции. Сформулированная и решенная задача считается основным вкладом Фибоначчи в развитие комбинаторики.

Рекурсия и числа Фибоначчи в математике

При помощи задачи о кроликах Фибоначчи предварил метод рекуррентных соотношений, как мощный метод решения комбинаторных задач. Один из вариантов по- простому увидеть рекурсию — посмотреть в зеркало, перед которым поставили еще одно зеркало. Повторное отражение зеркал создает видимость тоннеля. Разбор вложенных друг в друга матрешек тоже пример рекурсивного выполнения.

В математике, информатике, программировании без применения рекурсии не обойтись. Рекурсия чисел Фибоначчи — это правило (формула), по которому по нескольким последовательным элементам можно получить любой следующий член заданного числового ряда.

В методах определения функций и числовых рядов применяется математическая рекурсия. Примеры рекурсивных определений натуральных чисел, древовидных структур дискретной математики, функции вычисления факториала числа m, сортировки массива.

Один есть натуральное число; целое число, следующее за натуральным, есть натуральное число.
Дерево это множество, которое состоит из корня и соединенных с ним поддеревьев, они тоже являются деревьями. Дерево формализуется через самое себя. Рекурсия здесь конечна, т.к. поддерево имеет меньше узлов, чем включающее его дерево.
Факториал от m — это произведение всех натуральных чисел от 1 до m.

m!=1*2*3*..(m-1)*m. Требуемый m факториал вычисляется по значению предыдущего (m-1)!.

Золотое сечение

Эта идеальная пропорция, к которой каким-то образом стремятся природные объекты, создаются и описываются явления в искусстве, музыке. По сути, золотое сечение как связующее звено математических отношений, в приближениях иррационального числа рациональными числами, в бесконечных цепных дробях, в геометрии правильной пятиконечной звезды. Приближенное округление в процентах значения золотого деления дает результат отношения 62 % и 38%.

Проявление золотого сечения чисел Фибоначчи выражается в результате деления двух соседних элементов последовательности, который сходится (при возрастании m) и приближается к 1,618. Разделить на 2 целые доли с лучшим приближением к золотому сечению помогут элементы последовательности Фибоначчи. Например: в числе 13 разделяется на 8 и 5, в числе 21 — 13, 8.

Поделим отрезок LP(b) так, что точка N выполнит золотое сечение его таким образом, что LN: LP = NP:LN. Пусть LN=y (большая часть), тогда NP= b-y. Получается y:b=(b-y):y, т.е. y2=b*(b-y). Для определения y следует провести на отрезке дополнительное построение прямоугольного треугольника, используя среднее геометрическое длин отрезка и теорему Пифагора. Вычисляется значение y=( -1):2*b=0.62*b приближенно (t=0,618034).

Это лишь одно такое удивительное число, что обратное ему больше его самого ровно на 1, 1:t=1+t=1,618034. Решение уравнения t2 + t – 1 = 0 имеет единственный плюсовой корень. Используя это свойство числа, преобразовав выражение можно перейти к формуле числа t как бесконечной цепной дроби.

Золотая пропорция является иррациональной величиной. Числа Фибоначчи отражают целочисленные величины, отношение которых приближается к золотому делению. Эти две закономерности отражают неразрывность единых начал — непрерывного и дискретного.

Золотой прямоугольник и спираль Фибоначчи

Золотое деление характеризует в золотых прямоугольниках отношение – маленькая сторона (в) / длинная (а) равно длинная(а)/сумма короткой и длинной(а+в). Например, золотыми являются прямоугольники с длинами сторон числами Фибоначчи (55,34; 34,21; 21,13; и т.д. до 2,1).

Если в таком прямоугольнике (начиная с большего) отсечь квадрат (со стороной в), останется следующий меньший прямоугольник, большая сторона которого равна в, а малая (а-в). Продолжать произвольное число раз до самого малого квадрата. Дюрер (1525 г.) предложил простое построение: в каждый квадрат золотого прямоугольника вписывать четверть круга, образуются последовательно витки вокруг полюса. Получился частный случай логарифмической спирали – спирали Фибоначчи. Популярная линия Дюрера (Бернулли) – аппроксимация для золотой спирали (логарифмической).

При логарифмической (равноугольной) спирали для любой точки касательная образует с радиус-вектором одинаковый угол, а коэффициент роста означает изменение радиуса при повороте на 360°. Математики с момента открытия в 1638 году Декартом занимаются исследованием логарифмической спирали. Определено несколько схожих линий, не совпадающих точно с золотой. Коэффициент роста золотой (логарифмической) спирали равен f^4, где f=(+1)/2 - золотое сечение.

Понимать и разбираться в проблемах учит математика. Умению выделять главное, анализировать, отбрасывать лишнее обучаются на математических задачах и закономерностях. Важно при этом получать и чувствовать красоту гармонии формулировок, форм, собственных ассоциаций и аналогий.

История чисел Фибоначчи

Леонардо Пизано, по прозвищу Фибоначчи, — итальянский математик — родился в Пизе в 1170 году. Его отец работал в торговом порту на северо-востоке Алжира и часто путешествовал.

Фибоначчи изучал математику и во время обширных путешествий познакомился с индийско-арабской системой счисления. Оттуда математик и узнал о числовой последовательности, которую в древней Индии использовали в стихосложении.

Что такое числа Фибоначчи?

Числа Фибоначчи — это ряд, состоящий из целых чисел. Их особенность заключается в том, что каждый элемент представляет собой сумму двух предыдущих чисел.

Последовательность Фибоначчи начинается с 0 и 1. Продолжить ряд легко: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и так до бесконечности.

Математик обратил внимание на числовую последовательность, когда думал о разведении кроликов.

Кролики не умирают;
Кролики достигают половой зрелости за один месяц;
Срок беременности у кроликов – один месяц;
Достигнув половой зрелости, кролики-самки рожают ежемесячно кролика-самца и кролика-самку.

Схема разведения кроликов выглядит следующим образом:

Уже прослеживается закономерность. В конце каждого месяца количество пар кроликов будет больше, чем в предыдущем месяце ровно на столько, сколько пар было два месяца назад.

С точки зрения математики — это красивая последовательность. Но больший интерес для исследователей представляет не сам ряд, а частное соседних чисел, равное, примерно 1,618 для всех элементов ряда. Эта пропорция больше известна как золотое сечение.

Это соотношение можно найти во предметах, которые нас отгружают: гармония в гранях снежинок, в расположении лепестков цветов, ячеек ананаса, завитки раковин у улитки — все подчиняется правилу золотого сечения. Даже строение нашего тела гармонично: если измерить наш рост и разделить на расстояние от пояса до ступней или длину руки на расстояние от локтя до кончиков пальцев, получится известное нам соотношение 1,618.

Если мы видим человека и его внешность кажется красивой, то скорее всего пропорции его лица соотносятся с соотношением чисел Фибоначчи.

Природа полагается на эту врожденную пропорцию для поддержания баланса.

Финансовые рынки имеют ту же математическую основу, что и перечисленные природные явления. Давайте рассмотрим некоторые способы применения золотого сечения к финансам и покажем несколько диаграмм в качестве доказательства.

Числа Фибоначчи в трейдинге

Впервые изучением графиков биржевых котировок и поиском взаимосвязей занялся Ральф Hельсон Эллиотт, американский финансист. Ему удалось обнаружить в поведении фондового рынка особую гармонию. Как вы уже догадались – гармонию золотого сечения.

Мы рассмотрим четыре инструмента технического анализа, использующих последовательность Фибоначчи, активно применяемые трейдерами – это уровни, дуги, веер и временные зоны Фибоначчи.

Сначала поговорим об уровнях коррекции.

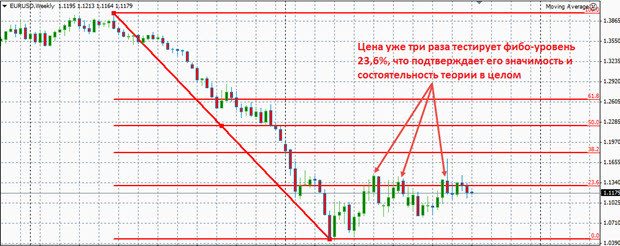
1. Коррекции Фибоначчи

Как это работает: берутся экстремальные точки на графике акций: нижний и верхний уровни цены долгосрочного тренда, и вертикальное расстояние между ними делится на коэффициенты Фибоначчи: 23,6%, 38,2%, 50%, 61,8% и 100%. После определения уровней соотношений на графике рисуются горизонтальные линии, представляющие уровни, указывающие на возможные уровни поддержки (цена перестает идти ниже) и сопротивления (цена перестает идти выше).

Откуда берутся эти значения процентов?

Как мы уже сказали, в последовательности чисел Фибоначчи каждое число примерно в 1,618 раза больше предыдущего. Например, 21/13 = 1,615, а 55/34 = 1,618.
Соотношение 61,8% получается делением одного числа в ряду на число, которое следует за ним. Например, 8/13 = 0,615 (61,5%), а 21/34 = 0,618 (61,8%).
Соотношение 38,2% получается путем деления одного числа в ряду на число, расположенное двумя позициями позже. Например, 5/13 = 0,385 (38,5%), а 55/144 = 0,3818 (38,2%).
23,6% рассчитывается путем деления одного числа в последовательности на число на три позиции выше. Например, 13/55 = 0,236 (23,6%), а 2/8 = 0,23076 (23,1%).
0% — это начало отката, а 100% — полный разворот исходной части движения.

Трейдеры используют уровни коррекции Фибоначчи для определения стратегических моментов для получения выгодной цены. Если тренд возрастает, то уровни коррекции Фибоначчи используются как потенциальные точки покупки при откатах, если тренд убывающий, то как точки входа для коротких продаж.

2. Дуги Фибоначчи

Дуги Фибоначчи учитывают как время, так и цену, также указывая на потенциальные области поддержки и сопротивления.

Поиск максимума и минимума графика — это первый шаг к построению дуг Фибоначчи. Затем рисуются три изогнутые линии, похожие на полукруги, на расстоянии 38,2%, 50% и 61,8% от желаемой точки. Полукруглые дуги показывают, где цена находит поддержку или сопротивление в будущем.

После роста цены дуги показывают до чего цена может откатиться, прежде чем снова начнет расти. После снижения цены дуги показывают, куда цена может подняться, прежде чем снова начнет падать.

3. Веера Фибоначчи

Веера Фибоначчи — это диагональные линии, образующие веер. Как и в предыдущих методах, сначала находятся максимум и минимум тренда. Если траектория возрастающая, то через точку максимума, если убывающие – через точку минимума условно проводится вертикальная линия.

Затем на линии отмечаются уровни: 38,2%, 50% и 61,8%. Дальше соединяются точки первого экстремума и точки, условно отмеченные на невидимой прямой. Получившиеся диагональные линии также указывают на области поддержки и сопротивления.

4. Временные зоны Фибоначчи

Временные зоны — это серия линий, параллельных оси ОУ, отстоящих друг от друга на расстоянии, пропорциональном элементам последовательности Фибоначчи (1, 1, 2, 3, 5, 8, 13 и т. д.).

Трейдер отмечает на графике очевидный ценовой тренд (его минимум и максимум). Расстояние между этими точками будет задавать единичный отрезок. Дальше рисуются прямые линии соответственно последовательности Фибоначчи: представьте, что вы строите график на координатной плоскости OXY. Ось OX разбита на длины единичного отрезка от 0 до бесконечности: 0, 1, 2, 3, 4, 5, 6, 7, 8…. и так далее.

Теперь вспомним, как выглядит ряд Фибоначчи: 0, 1, 2, 3, 5, 8…. Теперь именно в этих точках на оси OX и будут строиться вертикальные линии, соответствующие временным зонам. Каждая линия указывает время, в которое можно ожидать резкий скачок или спад цены.

Описанные инструменты далеко не единственные методы анализа графиков, использующих золоте сечение и числа Фибоначчи. Возможно, вы слышали и о таких инструментах, как клин, канал, спираль, также названных в честь Фибоначчи. Они отличаются способами построения и внешним видом, но смысл остается один — оценить области поддержки и сопротивления цены. Часто используют несколько методов одновременно для улучшения качества прогнозирования. Подробнее об инструментах, которые используются в трейдинге, можно узнать в бесплатной демо-версии книги по трейдингу.

Автор: Алексанян Андрон, эксперт SF Education

Читайте также: