Из какой последовательности складывается логическое дерево

Обновлено: 06.07.2024

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке "Файлы работы" в формате PDF

ВВЕДЕНИЕ

. для того чтобы усовершенствовать ум,

надо больше размышлять, чем заучивать.

Объект исследования: логические задачи, как источник развития математического мышления.

Предмет исследования: методы решения логических задач.

Гипотеза: решение логических задач – это не только очень увлекательный, но и крайне полезный способ время препровождения, как для школьников, так и для взрослых.

Для достижения цели мне необходимо решить следующие задачи:

- познакомиться с основными типами логических задач;

- изучить способы решения логических задач;

- на примерах конкретных задач выяснить, какие методы более эффективные;

- подготовить подборку наиболее интересных задач;

- исследовать, как решение логических задач влияет на интерес школьников к предмету математика, и какие методы решения наиболее эффективны.

Методы исследования: анализ литературы, анкетирование, статистический опрос, статистическая обработка полученных данных, анализ, сравнение и обобщение полученных результатов.

Новизна работы и её практическая ценность:

Логические задачи это не просто задачи, а это частички, решение которых остаётся надолго в нашей памяти. Все задачи – это частицы, из которых можно собрать пазлы, а из них картину, которой является сама математика. Так вот, я считаю, что задачи на логику – это основной пазл всей картины. И моя цель – доказать, что задачи на логику самые необычные и в тоже время самые интересные из всех математических задач.

Этапы работы:

- подобрать и изучить литературу и интернет - источники по теме;

- познакомиться с основными типами логических задач;

- изучить способы решения логических задач;

- выяснить, какие методы более эффективные;

- подготовить подборку наиболее интересных задач;

- исследовать, как решение логических задач влияет на интерес школьников к предмету математика и какие методы решения наиболее эффективны.

- провести анкетирование учащихся по данной проблеме.

- по результатам исследования сделать выводы.

1.1 ЧТО ТАКОЕ ЛОГИЧЕСКИЕ ЗАДАЧИ

Логика — это искусство приходить

к непредсказуемому выводу.Сэмюэл Джонсон

Чтобы разобраться, что такое логические задачи, необходимо узнать, а что же такое логика?

Слово "логика" происходит от греческого logos – "мысль", "слово", "разум", "закономерность".

В научной литературе можно найти следующие определения логики:

Теперь попробуем выяснить, а что же такое логические задачи?

Логические задачи – это занимательные игровые истории, где анализируется содержание с количественной, пространственной, качественной и временной точки зрения. (3)

Решение логически задач помогают развивать умение решать их другим нетрадиционным способом, где символика используется для замещения отношений (равенство - неравенство, больше - меньше, порядок следования, соответствие, логическое отрицание) и позволяют ориентироваться в реальности и получать о ней новую информацию, а при этом развивать умение делать умозаключения, как одну из логических форм мышления.

Логические задачи занимают особое место в среде математического мира. Они дают нам возможность проявить творческую активность, расширяют кругозор, развивают находчивость, смекалку, пробуждают интерес к знаниям и способствуют успешному интеллектуальному развитию.

Логическая задача ставит перед нами вопрос, на который непременно должен быть найден ответ. Причем успех зависит не только от правильности ответа, но и от быстроты реакции, способа решения. Именно при решении логической задачи можно демонстрировать свои способности, а так же удивлять сообразительностью и особенностью логического мышления (гибкость ума).

Развитие логического мышления – залог будущих стремительных успехов в школе, посредством овладения учащихся умениями анализировать, сравнивать, абстрагировать, обобщать. В процессе решения логических задач интеллектуальная деятельность учащихся связана с его действиями к окружающей действительности, предметам.

Математические отношения представлены разными способами (отрицание, детективный сюжет, количественные и качественные соотношения и др.) и решение логических задач осуществляется интересными методами: (5)

с помощью таблиц истинности;

Раскроем сущность методов и приведём примеры.

1.2 МЕТОДЫ РЕШЕНИЯ ЛОГИЧЕСКИ ЗАДАЧ

Метод рассуждений

Самый простой способ решения несложных задач заключается в последовательных рассуждениях с использованием всех известных условий. Выводы из утверждений, являющихся условиями задачи, постепенно приводят к ответу на поставленный вопрос. (13)

Идея метода: последовательные рассуждения и выводы из утверждений, содержащихся в условиях задач.

Преимущества метода: самый простой способ решения задач; нет необходимости в построении таблиц, схем.

Недостатки: применяется при решении только простых задач.

Пример 1: Возраст мамы и дочки в сумме составляет 98 лет. Дочь родилась, когда маме было 22 года. Сколько лет обеим?

Решение: так как разница в их возрасте 22 года (именно в этом возрасте у мамы родилась дочь), то 98 – 22 = 76 (лет). Это удвоенный возраст дочери, тогда 76 : 2 = 38 (лет). Значит, матери 98 – 38 = 60 (лет).Пример 2: Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский и арабский. На вопрос, какой язык изучает каждый из них, один ответил: "Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский". Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из молодых людей?

Решение: Имеется три утверждения. Если верно первое утверждение, то верно и второе, так как юноши изучают разные языки. Это противоречит условию задачи, поэтому первое утверждение ложно. Если верно второе утверждение, то первое и третье должны быть ложны. При этом получается, что никто не изучает китайский. Это противоречит условию, поэтому второе утверждение тоже ложно. Остается считать верным третье утверждение, а первое и второе — ложными. Следовательно, Вадим не изучает китайский, китайский изучает Сергей.

Ответ: Сергей изучает китайский язык, Михаил — японский, Вадим — арабский.

Метод таблиц истинности

Основной прием, который используется при решении текстовых логических задач, заключается в построении таблиц. Таблицы не только позволяют наглядно представить условие задачи или ее ответ, но в значительной степени помогают делать правильные логические выводы в ходе решения задачи. (5)

Идея метода: оформлять результаты рассуждения в виде таблицы.

- возможность контролировать процесс рассуждений;

- возможность формализовать некоторые суждения;

Недостатки: применяется для решения только определённых типов задач.

Пример: Игорь, Петя и Саша ловили рыбу. Каждый из них поймал либо ершей, либо пескарей, либо окуней. Кто из них каких поймал рыб, если известно:

1) колючие плавники есть у окуней и ершей, а у пескарей их нет;

2) Игорь не поймал ни одной рыбы с колючими плавниками;

3) Петя поймал на 2 окуня больше, чем поймал рыб Игорь?

Зная 1 и 2 высказывания, можно сделать вывод, что Игорь поймал пескарей.

Зная, что Петя поймал на 2 окуня больше, чем поймал рыб Игорь, можно сделать вывод, что Петя поймал окуней, тогда второй столбец заполнится:

Получаем, что Саша поймал ершей, так как каждый поймал один вид рыб.

Ответ: Игорь поймал пескарей, Петя - окуней, Саша - Ершей.

Метод блок-схем

Это задачи, в которых с помощью сосудов известных емкостей требуется отмерить некоторое количество жидкости, а также задачи, связанные с операцией взвешивания на чашечных весах. Простейший прием решения задач этого класса состоит в переборе возможных вариантов. Понятно, что такой метод решения не совсем удачный, в нем трудно выделить какой-либо общий подход к решению других подобных задач. (12)

Более систематический подход к решению задач "на переливание" заключается в использовании блок-схем. Суть этого метода состоит в следующем. Сначала выделяются операции, которые позволяют нам точно отмерять жидкость. Эти операции называются командами. Затем устанавливается последовательность выполнения выделенных команд. Эта последовательность оформляется в виде схемы. Подобные схемы называются блок-схемами и широко используются в программировании. Составленная блок-схема является программой, выполнение которой может привести нас к решению поставленной задачи. Для этого достаточно отмечать, какие количества жидкости удается получить при работе составленной программы. При этом обычно заполняют отдельную таблицу, в которую заносят количество жидкости в каждом из имеющихся сосудов.

Идея метода: описать последовательность выполнения операций, определять порядок их выполнения и фиксировать состояния.

- наглядность представления последовательности действий процесса;

- все этапы процесса представлены в виде отдельных блоков;

- определенность последовательности действий, ограниченная прямыми связями между блоками схемы;

- возможность записи в блоки последовательности действий процесса;

- возможность повторения отдельных этапов процесса;

- наличие обратных связей.

Недостатки: применяется для решения только определённых типов задач.

Пример: Есть 8 литровый сосуд, полный воды.Как отлить 4 литра, если есть пустые емкости объемом 3 и 5 литров? Решение:

Графический метод решения логических задач

Точки называются вершинами графа, а линии— рёбра.

Графический метод решения логических задач предназначен для наглядного представления информации в форме графов, для построения которых необходимо сначала определить вершины графа и соединить их по правилам, образовав ребра.

Количество рёбер, выходящих из вершины графа, называется степенью вершины.

Идея метода: Оформлять результаты логических рассуждений в виде графов.

- применяется для нахождения соответствий между несколькими типами объектов;

- возможность обобщить метод на широкий класс задач;

Недостатки: запутанное условие (из-за соединяющих графы линий); применяется для решения определённых типов задач.

Пример: Пятеро учёных, участвовавших в научной конференции, обменялись рукопожатиями. Сколько всего было сделано рукопожатий?

Решение: Обозначим ученых вершинами графа и проведем от каждой вершины линии к четырем другим вершинам. Получаем 10 линий, которые и будут считаться рукопожатиям

Ответ: было сделано 10 рукопожатий.

Метод кругов Эйлера

Круги Эйлера — это геометрическая схема. С ее помощью можно изобразить отношения между подмножествами (понятиями), для наглядного представления.

Метод Эйлера является незаменимым при решении некоторых задач, а также упрощает рассуждения. (5)

Идея метода: определить количество элементов, обладающих общими свойствами.

- необязательно знание формул;

Недостатки: применяется для решения определённых типов задач; необходимость в построениях.

Пример 1: Каждый ученик в классе изучает либо английский, либо французский язык, либо оба эти языка. Английский язык изучают 25 человек, французский - 27 человек, а то т и другой - 18 человек. Сколько всего учеников в классе?

Решение: Английский язык изучают 7 учеников, французский - 9, и тот и другой 18, получаем, что всего в классе 7+9+18 = 34 ученика в классе.

Ответ: в классе 34 ученика.

Пример 2: Все мои друзья занимаются каким-нибудь видом спорта. 17 из них увлекаются футболом, а 14 — баскетболом. И только двое увлекаются и тем и другим видом спорта. Угадайте, сколько у меня друзей?

Решение: Обратимся к кругам Эйлера:

1.Изобразим два множества, так как два вида спорта. В одном будем фиксировать друзей, которые увлекаются футболом, а в другом — баскетболом2.Поскольку некоторые из друзей увлекаются и тем и другим видом спорта, то круги нарисуем так, чтобы у них была общая часть (пересечение)

17 из них увлекаются футболом, а 14 — баскетболом. И только двое увлекаются и тем и другим видом спорта. Расставить числа, согласно условию задачи:

Ответ: 29 друзей

1.3 Синквейны основных методов логических задач

Синквейн (от фр. cinquains, англ. cinquain) — это творческая работа, которая имеет короткую форму стихотворения, состоящего из пяти нерифмованных строк.

Синквейн – это не простое стихотворение, а стихотворение, написанное по следующим правилам:

1 строка – одно существительное, выражающее главную тему cинквейна.

2 строка – два прилагательных, выражающих главную мысль.

3 строка – три глагола, описывающие действия в рамках темы.

4 строка – фраза, несущая определенный смысл.

5 строка – заключение в форме существительного (ассоциация с первым словом).

Метод рассуждений

Мыслить, рассуждать, решать

Заставляет рассуждать над решением задачи

Метод таблиц истинности

Оформлять, контролировать, решать

Возможность контролировать процесс рассуждения

Метод блок-схем

Составлять, обрабатывать, решать

Определённая последовательность действий

Оформлять, соединять, решать

Дерево логических условий – это целая картина

Метод кругов Эйлера

Построить, рассуждать, решать

Простота решения задач – это круги Эйлера

Вывод: составлять cинквейн очень просто и интересно. И к тому же, работа над созданием синквейна развивает образное мышление.

2.1 ИЗУЧЕНИЕ УМЕНИЯ РЕШАТЬ ЛОГИЧЕСКИЕ ЗАДАЧИ

Для ответа на вопрос, как решение логических задач влияет на интерес школьников к предмету математика, и какие методы решения наиболее эффективны мною была проведена следующая работа:

- рассказал ребятам, что такое логические задачи, какими методами они решаются;

- подобрал по одной задаче по каждому методу логических задач:

Задача 1:Четыре брата Юра, Петя, Вова, Коля учатся в 1,2,3,4 классах. Петя- отличник, младшие братья стараются брать с него пример. Вова учится в 4 классе. Юра помогает решать задачи брату. Кто в каком классе учиться?

Задача 3:Как, имея пятилитровое ведро и девятилитровую банку, набрать из реки ровно три литра воды?

и предложил решить их учащимся 6 Б и В классов;

- после попросил ребят ответить на вопросы анкеты: 1. Влияет ли решение логических задач на развитие интереса у школьников к предмету математика? 2. Какие методы решения наиболее эффективны? 3. Развивает ли умственное мышление, память, внимание умение решать логические задачи? 4. Легко ли вам даётся решение логических задач? 5. Умение решать логические задачи помогут вам лучше учиться?

Учащиеся решили задачи с удовольствием. Справились все. Анализируя результаты анкетирования, можно подвестиитог, что решение логических задач влияет на развитие интереса у школьников к уроку математики. Также выяснилось, что наиболее эффективный метод решения логических задач – метод рассуждений.

Если уметь решать логические задачи, то можно лучше учиться, так как развивается память, мышление, ум, внимание. Школьникам обязательно нужно научиться решать логические задачи. С логикой и логическими задачами мы сталкиваемся не только в школе на уроках математики, но и на других предметах.

Глава II. Заключение

В ходе работы над проектом я пришёл к выводам:

- наиболее эффективный метод решения логически задач является метод рассуждений;

- решение логических задач влияет на развитие интереса у школьников к уроку математики.

Сформулированная гипотеза о том, что решение логических задач – это не только очень увлекательный, но и крайне полезный способ время препровождения, как для школьников, так и для взрослых, полностью подтвердилась.

Работая над проектом, я научился работать с различными источниками информации. Узнал, какие существуют методы решения логических задач. Составил, обработал и анализировал анкеты учащихся.

Практическая значимость моего проекта нашла своё отражение в двух продукта:

- в сборнике задач; - в составлении буклета.

Сборник задач содержит 45 решенных логических задач. В среднем по 9 задач каждого метода. Каждая задача имеет объяснение и решение. Данный сборник будет полезен как учащимся 5 - 9 классов так и взрослым. Буклет поможет всем желающим научиться решать логические задачи разными методами.

Считаю, что информация в буклете и составленные задачи помогут ребятам лучше подготовиться и сдать итоговую аттестацию за курс основной школы.

В дальнейшем я планирую попробовать сам составлять логические задачи, так как это интересно и занимательно, развивает память, мышление, внимание.

СПИСОК ЛИТЕРАТУРЫ

1. Андреева Е.В., Босова Л.Л., Фалина И.Н. Математические основы информатики. Элективный курс. – М.: Лаборатория базовых знаний, 2007;

2. Гейн А.Г. Математические основы информатики. Лекции 5–7 – М.: Педагогический университет “Первое сентября”, 2008;

3. Лыскова В.Ю., Ракитина Е.А. Логика в информатике – М.: Лаборатория Базовых Знаний, 2001;

4. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В. Арифметика: Учебник для 6 кл. общеобразовательных учреждений / - 2-е изд. – Москва: Просвещение, 2002;

5. Рыбак К.Ю. Методы решения логических задач // Сборник материалов по результатам проведения недели математики в ДВГГУ. Выпуск 1 / под ред. М.А. Кисляковой. – Хаба- ровск: Изд-во Дальневост. гос. гуманит. ун-та, 2015;

6. Спивак А.В. Тысяча и одна задача по математике. - М.: Просвещение, 2005;

7. Фарков А.В. Математические олимпиады в школе. 5-11 классы – М.: Айрис-пресс, 2008;

8. Шарыгин И. Ф., Шевкин А. В. Математика: Задачи на смекалку: Учеб. пособие для 5 – 6 кл. общеобразоват. учреждений. – 5-е изд. – М.: Просвещение, 2000.

Тип данных дерево обычно отсутствует в универсальных языках программирования, и нужно его моделировать программно. Так же, как и в списках, цепная структура дерева будет состоять из динамически порождаемых элементов, в которых предусмотрены ссылки на очередные компоненты структуры:

struct node

char key;

struct node* 1;

struct node* r; >

Динамическая структура выглядит так: >>>>>>>

Рассмотрим программу построения дерева из n вершин, значения которых поступают из входного текстового файла input. Если нам нужно построить из этих вершин какое- нибудь дерево, то можно первую из них сделать корнем, вторую правым поддеревом, третью правым поддеревом правого поддерева, и т. д. В результате получим линейное дерево (список) максимальной глубины (n). Интереснее обратная задача: построить из этих же вершин дерево минимальной глубины. Для этого при построении дерева надо добиться его равномерного заполнения (ау. сплошное турнирное представление!), размещая приходящие вершины поровну слева и справа от каждой вершины по следующему рекурсивному(!) правилу:

1)взять одну вершину в качестве корня:

2)построить тем же способом левое поддерево с = n_l div 2 вершинами;

3)построить тем же способом правое поддерево сn_r = n — n_l — 1 вершиной.

25 Двоичное дерево. Физическое представление. Прошивка.

На массиве: цельный кусок памяти, на первом месте корень, на 2м и 3м – его левый и правый сыновья, а далее – по паром сыновья каждого родителя, т.е. Сыновья i-го родителя лежат на местах 2i и 2i+1 (j-ый элемент i-го уровня находится на месте 2^(j-1) + j – 1.

Основным неудобством сплошного представления дерева является высокая цена вставки и удаления элементов + перерасход памяти.

Для деревьев можно использовать рекурсивные ссылочные представления, которые были разработаны для списков, но с той лишь разницей, что указатели вперёд и назад по линейной структуре теперь направляются к левому и к правому поддеревьям соответственно.

Динамическая структура: каждый элемент указывает на место своих сыновей

Прошитые бинарные деревья – В прошитых бинарных деревьях вместо пустых указателей используются специальные связи-нити и каждый указатель в узле дерева дополняется однобитовым признаком ltад и rtag, соответственно. Признак определяет, содержится ли в соответствующем указателе обычная ссылка на поддерево или в нем содержится связь-нить.

Связь-нить – в поле l указывает на узел-предшественник при обратном обходе, а в поле r – на узел-приемник.

Для прошитых деревьев можно выполнить не рекурсивный обход без использования стека.

Прошитое дерево линеаризовано и может быть помещено в очередь или список => можно применить итераторы для обработки, т.к функциональность совпадает.

Среди прошитых деревьев важный класс составляют правопрошитые деревья, т. е. прошитые бинарные деревья, у которых используется только правая связь-нить, а в поле / содержится либо обычный указатель, либо пустой указатель. Поле ltag в таком случае не используется. (картинка справа: дерево для арифметических операций)

26 Алгоритмы обхода деревьев.

Обход дерево – просматривание дерева по определённому алгоритму так, что все вершины будут просмотрены.

Для бинарного дерева:

Iпрямой обход (сверху вниз; КЛП; корень прежде; preorder) 1) если дерево пусто – конец обхода 2) берём корень 3) обходим левое поддерево 4) обходим правое поддерево

II обратный обход (слева направо; ЛКП; корень между; inorder) 1) если дерево пусто – конец обхода 2)обходим левое поддерево 3) берём корень 4)обходим правое поддерево

III концевой обход (снизу вверх; ЛПК; корень в конце; posorder) 1) если дерево пусто – конец обхода 2) обходим левое поддерево 3) обходим правое поддерево 4) берём корень

Для обычного дерева:

Iпоиск в глубину: 1) если дерево пусто – конец обхода

2) берём корень 3) ищем в глубину для поддерева старшего сына 4) ищем в глубину для поддерева следующего брата

IIпоиск в ширину: 1) поместить в пустую очередь корень дерева 2) если очередь узлов пуста – конец обхода 3) извлечь первый элемент из очереди и поместить в конец всех его сыновей 4) вернуться к п. 2)

27 Особенности представления и обработки деревьев общего вида (преобразование к двоичному. )

Сплошное представление деревьев удобно пояснить на примере турнирного дерева с фиксированной структурой. Считая, что участники турнира образуют полные пары нужной кратности, введём жёсткое размещение элементов дерева в массиве. В первом элементе массива разместим корень дерева, во 2-ом и 3-ем — его левого и правого потомков. Далее поместим пары потомков потомков и т. д. Сыновья элемента дерева с индексом i хранятся в элементах массива с индексами 2i и 2i + 1. Согласно данной схеме размещения, j-ып элемент i-ого уровня имеет индекс 2 i -[ + j — 1.

Основным неудобством сплошного представления дерева является высокая цена вставки и удаления элементов. Не мал и перерасход памяти на пустые элементы. Для деревьев можно использовать рекурсивные ссылочные представления, которые были разработаны для списков, но с той лишь разницей, что указатели вперёд и назад по линейной структуре теперь направляются к левому и к правому поддеревьям соответственно.

В представлении бинарного дерева содержатся два указателя на левое и правое поддеревья (обозначим их l и г, соответственно). У листьев дерева оба эти указателя пустые. Поскольку в бинарном дереве, как правило, около половины узлов являются листьями (если не рассматривать вырожденные случаи), то такое представление оказывается неэкономичным с точки зрения расхода памяти .

В прошитых бинарных деревьях вместо пустых указателей используются специальные связи-нити и каждый указатель в узле дерева дополняется однобитовым признаком ltag и rtag, соответственно. Признак определяет, содержится ли в соответствующем указателе обычная ссылка на поддерево или в нем содержится связь-нить.

Деревья выражений

Деревья выражений – деревья, в узлах которых стоят элементы выражения (+, _, *, /, a = const, x != const).

при прямом обходе получаем префиксную (польскую) форму: * + a / bc – d * ef (КЛП – Левый-Корень-Правый)

при обратном обходе получаем инфиксную (обычную) форму без скобок: a + b / c * d – e * f(ЛКП)

при концовом обходе получаем постфиксную (обратную польскую) форму: abc / + def * - *(ЛПК)

Пример1:Выражение (1+2)*4+3 в ОПН может быть записано так: 1 2 + 4 × 3 +

Вычисление производится следующим образом (указано состояние стека после выполнения операции):

Ввод Операция Стек

1 поместить в стек 1

2 поместить в стек 1, 2

4 поместить в стек 3, 4

3 поместить в стек 12, 3

Результат: 15, в конце вычислений находится на вершине стека.

Пример2: для вычисления деревья выражений можно применить алгоритм Дейкстры основанный на применении стеков с приоритетами и польской записью:

30 Деревья поиска. Дерево поиска – это такое дерево, для каждого узла t которого выполняются следующие условия: 1) ключи всех узлов в левом поддереве меньше значения t 2) ключи всех узлов в правом поддереве больше значения t.

Двоичные деревья часто употребляются для представления множеств данных, элементы которых должны быть найдены по некоторому ключу (нулю данных). В дереве легко и быстро найти элемент с заданным ключом: начиная от корня, двигаемся к левому или правому поддереву на основании лишь сравнения с ключом текущей вершины. По построению дерева поиска, переходя к одному из поддеревьев, мы автоматически исключаем другое поддерево с остальными узлами. Далее таким делением и исключением мы доходим до исключения подавляющего большинства вершин и нахождения нужных.

Дерево поиска может быть использовано для упорядочивания данных. Для этого надо разместить эти данные в дереве поиска, а потом составить в результате его обхода упорядоченную последовательность. Но для решения этой задачи обычное дерево поиска не подходит: оно не допускает вхождения равнозначных элементов. Поэтому всякий новый элемент теперь должен быть включён в дерево. Для этого случай х = р^ .key необходимо рассматривать вместе с одним из других. Если его объединить с х > р^.кеу, то порядок следования элементов с одинаковыми ключами совпадёт с хронологией их поступления в дерево. Возможность сочетания поиска и упорядочивания растущего множества данных, предоставляемая деревом поиска с включениями, даёт новое качество по сравнению с хранением данных как в списках, так и в массивах. Например, этим способом можно эффективно решить задачу составления таблицы перекрёстных ссылок слов текста .

31 Сбалансированные деревья поиска.

Т.к. введение новой вершины в идеально сбалансированное дерево его разбалансирует, то решили делать балансировку после вставки.

AVL-дерево – то дерево, высота поддеревьев каждой из вершин которого отличается не более, чем на единицу.

( идеально сбалансированное дерево является AVL-деревом)В AVL-дереве можно найти искомую вершину, добавить новую или удалить старую.

Схема алгоритма включения в сбалансированное дерево такова:

1. поиск элемента в дереве; 2. включение новой вершины и определение результирующего показателя сбалансированности; 3. отход по пути поиска с проверкой показателя сбалансированности для каждой проходимой вершины, балансируя в необходимых случаях соответствующие поддеревья.

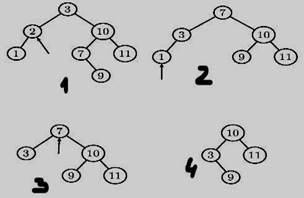
Сложность балансировки оправдана тогда, когда поиск данных происходит значительно чаще¸ чем вставка. Двудетные вершины дерева обрабатываются путем замены самой правой вершины из левого поддерева. Удаление элементов выглядит так:

32 Простые методы поиска.

Линейный поиск – последовательный просмотр массива как списка (цикл). Поиск происходит за O(N). Индексация начинается с 0. Ускорить поиск можно с помощью барьерного элемента. Его следует поместить в N+1-ый элемент массива. Этот метод поиска единственный для структур данных со строго последовательным доступом.

int function LinearSearch (Array A, int L, int R, int Key);

Рассмотрим разновидность двоичного дерева которую мы назовем логическим деревом. В этом дереве каждый уровень полностью заполнен, за исключением, возможно, последнего (самого глубокого) уровня. При этом, все вершины последнего уровня находятся максимально слева. Дополнительно, каждая вершина дерева имеет ноль или двоих детей.

Каждая вершина дерева имеет связанное с ней логическое значение (1 или 0). Кроме этого, каждая внутренняя вершина имеет связанную с ней логическую операцию ("И" или "ИЛИ"). Значение вершины с операцией " И " - это логическое " И " значений ее детей. Аналогично, значение вершины с операцией " ИЛИ " - это логическое " ИЛИ " значений ее детей. Значения всех листьев задаются во входном файле, поэтому значения всех вершин дерева могут быть найдены.

Наибольший интерес для нас представляет корень дерева. Мы хотим, чтобы он имел заданное логическое значение v, которое может отличаться от текущего. К счастью, мы можем изменять логические операции некоторых внутренних вершин (заменить " И " на " ИЛИ " и наоборот).

Дано описание логического дерева и набор вершин, операции в которых могут быть изменены. Найдите наименьшее количество вершин, которые следует изменить, чтобы корень дерева принял заданное значение v. Если это невозможно, то выведите строку "IMPOSSIBLE" (без кавычек).

В первой строке входного файла находятся два числа n и v (1 ≤ n ≤ 10000, 0 ≤ v ≤ 1) - количество вершин в дереве и требуемое значение в корне соответственно. Поскольку все вершины имеют ноль или двоих детей, то n - нечетное. Следующие n строк описывают вершины дерева. Вершины нумеруются с 1 до n. Первые (n-1)/2 строк описывают внутренние вершины. Каждая из них содержит два числа - g и c, которые принимают значение либо 0, либо 1. Если g=1, то вершина представляет логическую операцию "И", иначе она представляет логическую операцию "ИЛИ". Если c=1, то операция в вершине может быть изменена, иначе нет. Внутренняя вершина с номером i имеет детей 2i и 2i+1. Следующие (n+1)/2 строк описывают листья. Каждая строка содержит одно число 0 или 1 - значение листа.